¿Qué es una distribución
normal?
La distribución normal representa una de las "verdades elementales" acerca de la naturaleza de la realidad. Se ha verificado empíricamente que muchos fenómenos naturales se distribuyen normalmente.
|
Algunas variables psicológicas y sociales no se
distribuyen normalmente y, por lo tanto, no deberían ser sujetas,
directamente, a pruebas estadísticas que demanden una distribución
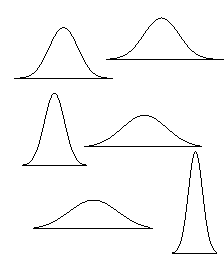
normal de los datos. Aunque la forma de la campana puede variar la distribución
siempre debe ser simétrica con más casos concentrados en el centro y menos en
los extremos.
|
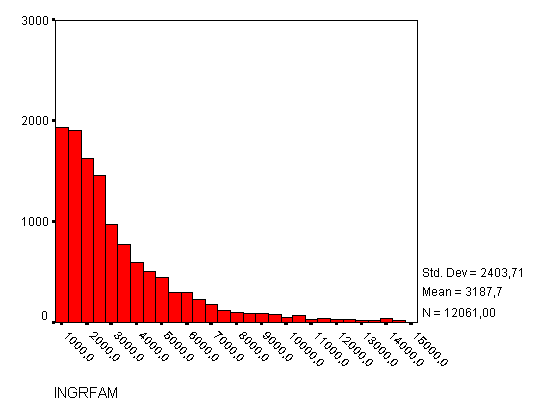
Distribución del ingreso de un
segmento
de la población salvadoreña.
1999.
|
En una distribución perfectamente normal los casos se distribuyen de la siguiente manera:

El 68,26% del área total de la
curva cae entre más menos 1 desviación estándar. Exactamente 95,44% del área
cae entre más menos 2 desviaciones estándares y exactamente 99,74% del área cae
entre más menos 3 desviaciones estándares.
La forma exacta de la
distribución normal (la característica curva con forma de campana) se define
por una función que tiene solamente dos parámetros: la media y la desviación
estándar. La media es el valor que con mayor probabilidad aparecerá en una
medida. La desviación estándar refleja lo abierta o cerrada que es la campana
de Gauss correspondiente. Una distribución muy cerrada se corresponde con una
serie de medidas muy poco dispersas. Por el contrario si la distribución es
abierta, la desviación estándar es grande.
Manteniendo el valor del
promedio igual, otorgue distintos valores para la desviación estándar:
|
|
|
|
Si no puede el cuadro
anterior.... Vínculo
a una animación interactiva
Mucho de los tests estadísticos se han diseñado bajo
las premisas de una distribución normal. Algunos tests, los no paramétricos no
asumen que los datos se distribuyan normalmente, sin embargo estos tests son
menos poderosos o robustos que los tests paramétricos.
¿Cómo comprobar si una
distribución es normal?
a) Observándola simetría del
histograma de la distribución.
b) En una distribución normal la
media, la moda y la mediana son iguales.
c) Calculando la simetría (en SPSS: Skewness) de la
distribución. En una distribución normal perfecta la asimetría debería ser 0 y
las desviaciones respecto al cero indicarían distintos niveles de asimetría. Un
valor absoluto mayor que 1 en el índice de asimetría estaría indicando que la
distribución de los datos no es normal.
¿Qué es el puntaje Z o puntaje
estandarizado?
Los puntajes Z son transformaciones
que se pueden hacer a los valores o puntuaciones de una distribución normal,
con el propósito de analizar su distancia respecto a la media, expresándolas en
unidades de desviación estándar. Un puntaje Z nos indica la dirección y grado
en que un valor individual obtenido se aleja de la media, en una escala de
unidades de desviación estándar.
Por ejemplo, si la edad promedio
del grupo de estudiantes de psicología es de 23 años y la desviación estándar
es igual a 4, un estudiante de 27 años se ubicaría 1 desviación estándar ( Z=1
) respecto al promedio.
La fórmula para transformar un
valor de una distribución normal en una unidad de desviación estándar es:
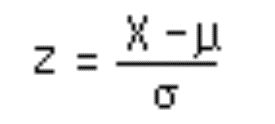
Donde X es la puntuación o valor a
transformar, m es la media de la distribución original, y s la desviación estándar de la misma distribución. El resultado Z es la
puntuación transformada a unidades de desviación estándar.
Al aplicar la fórmula siempre se
produce una nueva variable con una media de cero y una desviación estándar de uno. Sin embargo, la forma de la
distribución no se verá afectada por la transformación.
Digite distintos valores para la
media, desviación estándar y puntaje z y observe los cambios:
|
|
|
|
¿Cuándo es útil calcular el
puntaje Z?
Es útil cuando comparo dos
variables medidas en escalas diferentes (por ejemplo, peso y estatura) o cuando
el puntaje original no se entiende con claridad en su forma bruta.
Ejemplo:
Los siguientes gráficos muestran la utilidad del puntaje Z. Los datos son opiniones de profesores sobre distintos aspectos del funcionamiento organizacional de sus escuelas y el tipo de colegio de acuerdo a su rendimiento en una prueba de ingreso a la universidad. Mientras el primer gráfico muestra las puntuaciones brutas el segundo presenta los datos convertidos en putuaciones Z.
|
Sub-escalas por tipo de escuela. Puntaje directo. |
El primer gráfico muestra el promedio en cada subescala por Tipo de escuela (rendimiento alto y bajo). Se observa que no hay muchas diferencias entre los tipos de escuela. Además, aparentemente, el gráfico parece indicar que el "Liderazgo del director" es la dimensión mejor evaluada en opinión de los profesores. En este gráfico se pasó por alto que cada sub-escala tenía un rango distinto de puntuaciones posibles. Así mientras en la escala "Cooperación entre profesores" habían solamente 5 preguntas con un puntaje máximo posible de 20, la sub-escala de "Liderazgo del director" se construyó con la respuesta a 20 preguntas con un puntaje máximo posible de 80. El problema es que se presentan en un mismo plano variables medidas de distinta manera. El puntaje Z ayuda a superar este problema y nos da una mejor imagen del comportamiento de las variables en este estudio. |
| Este 2do gráfico muestra los mismos datos del gráfico anterior pero transformados en puntuaciones estandarizadas (puntaje Z). Esta representación permite constatar la distintas tendencias entre ambos grupos a la vez que proporciona una unidad de medida común que permite poner todas las variables en el mismo plano. |
Sub-escalas por tipo de escuela. Puntaje Z. |
Datos de los ejemplos: Datos de profesores; Sintaxis para la obtener los gráficos.
Álvaro Carrasco
UAH-Chile-2003