Gráfico 1
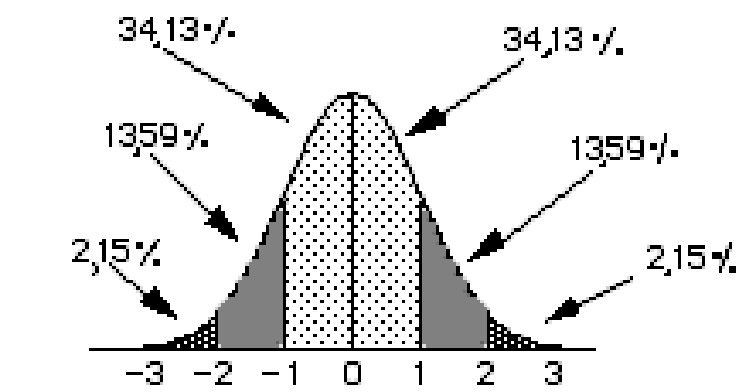
| La distribución normal es siempre la misma: simétrica, con un gran porcentaje en el centro de la distribución y algunos pocos casos en los extremos. Hablamos claro de una distribución teórica y perfectamente normal. En la práctica nunca se encuentra una variable que sea exactamente igual a nuestra distribución normal teórica. En cualquier caso, mientras una variable no se aparte demasiado de la normalidad es posible utilizar una serie de procedimientos estadísticos que se fundamentan en la distribución normal. |
Gráfico 1
|
|
La distribución normal es una distribución de probablidad. Lo que significa que podemos decir cuál es la probabilidad de ocurrencia de un evento aleatorio proveniente de una población normal. Por ejemplo, mirando el gráfico 1, podemos decir que la probabilidad de extraer aleatoriamente un caso que se encuentre entre la media y -1 desviación estandar es de 34,13%. ¿Cierto? Si lo que que se sabe es la probabilidad de un evento, digamos que sabemos que el caso elegido tenía menos de un 2,15% de probabilidades de ocurrir eso significa que debe haber obtenido una puntuación Z mayor a 2 o menor que -2. Siguiendo esta lógica y usando el Gráfico 1, ¿Cuál sería la probabilidad de ocurrencia de un caso con una puntuación Z igual 1,5? ¿Cuál sería el puntaje z de un caso que está encima del 84.26% del resto de la población? ¿Cuál es la probabilidad de ocurrencia de dicho caso? Estas estimaciones pueden hacerse con mucha mayor precisión si se ocupan las computadoras o las tablas de probabilidades y puntuaciones Z. Abajo tenemos una de estas tablas (Tabla 1). Esta tabla permite ientificar el puntaje Z para una probabilidad dada. La probabilidad se obtiene sumando al valor de la columna izquierda el valor del encabezado de la columna. Por ejemplo, la probabilidad del 8% se obtiene al elegir el valor .00 de la columa izquierda y buscar el valor .08 en el encabezado de la columna. Se considera este 8% distribuído en los dos extremos de la desviación, 4% en el extremo inferior y 4% en el extremos superior. Tabla 1 Puntaje Z en función de la probabilidad (p)
El punto de intersección en la tabla indica que una probabibilidad de 0,04 se espera a partir del -1.75 y otro 0,04 desde el 1.75 (zonas en rojo en el Gráfico 2), dándo como total p=0,08. Gráfico 2
|
¿Cuál sería el puntaje Z para una p=0,05 y p=0,01? Haga un gráfico (curva normal) en que se muestren la ubicación de Z para p=0,05 y p=0,01? Puede hacerlo manualmente o usando alguno de los siguientes recursos: Applet 1 (si funciona....) o Applet 2
Usando los mismos datos del curso del alumno 20 usados cuando estudiamos las puntuaciones estandarizadas, identifique el puntaje Z del alumno 17 y el valor p correspondiente. ¿Qué significa esto? Haga un gráfico (curva normal) en que se muestren la ubicación de Z para el puntaje del alumno 17.
T de student
En el caso de los alumnos 17 y 20 de nuestro curso de matemáticas, calcular la probabilidad era un asunto relativamente fácil ya que, conocida la media y la desviación estándar del grupo, fácilmente podemos calcular el puntaje Z y la probabilidad correspondiente si la distribución es normal. El problema es que en investigación, con mucha frecuencia, no se conocen los datos (media y desviaciones estándar) de las poblaciones. La t de student es una prueba que ayuda a estimar los valores poblacionales a partir de los datos muestrales. La t de student ayuda a pronosticar la probabibilidad de que dos promedios pertenezcan a una misma población (en el caso en que las diferencias no sean significativas) o que provengan de distintas poblaciones (en el caso que la diferencias de promedios sea significativas). Pensemos el siguiente ejemplo.
|
Grupo
1 N=20 hombres y 20 mujeres adultos entre 20 y 60 años
|
Grupo 2 N=20 hombres y 20 muejres
adultos entre 2o y 60 años
|
 |
|
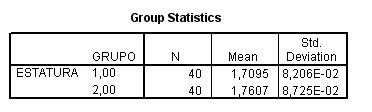
¿Es posible que estos sean dos grupos de chilenos? ¡Por supuesto que es posible! Por ejemplo yo pude haber conformado los grupos intencionalmente para que muestren una diferencia promedio. Claro que esta sería una situación que no ocurre en una investigación; uno no manipula las diferencias sino que controla ciertas variables (las variables extrañas o intervinientes), manipula otras condiciones (variable independiente) y observa si hay diferencia (comportamiento de la variable dependiente). En realidad, para evitar sesgos y controlar la intromisión de variables extrañas en la selección de los casos, los investigadores recurren a una selección aleatoria de los casos (hasta donde sea posible) y una asignación aleatoria a las condiciones experimentales. Entoces, reformulemos la pregunta: ¿es posible que estos grupos elegidos aleatoriamente sean de la misma población? ¡Por supuesto que es posible! Sabemos que es posible pero eso no sirve de mucho al científico a quién le interesa tener una mayor certeza. En otras palabras a los investigadores no solo les interesa si es posible sino también cuál es la probabilidad de que pertenezcan a la misma población. Si conocieramos el promedio y la desviación estándar de la estatura de todos los chilenos podríamos calcular el puntaje z de cada sujeto en nuestros grupos y, luego, promediar las puntuaciones z para cada grupo, lo que nos permitiría estimar la probabilidades correspondientes. Sin embargo, tal como suceda con frecuencia, no conocemos la media y la desviación estándar de la estatura de todos los chilenos. Afortunadamente eso no es problema ya que usando el procedimiento estadístico desarrollado por Gosset y conocido como t de Student, es posible hacer estimaciones bastantes precisas a partir de los datos de las muestras (Grupo 1 y Grupo 2)
| La prueba t de student se accede en SPSS a través del menú de "Comparación de medias", si quisieramos hacer el análisis para el ejemplo de la estatura que estamos viendo, deberíamos selecciones el sub-menú "T-test para muestras independientes" (el "T-test para muestras dependientes" sirve cuando a un mismo grupo se le mide 2 veces). Este análisis nos arroja una tabla como la siguiente: | Hacer el ejercicio con los datos en SPSS |
Tabla 1. Ejemplo de salida de SPSS para el análisis de t de student

Se ha incluído dentro de la elipse roja los valores a atender en la tabla. El primer valor de izquierda a derecha "Sig" indica la probabilidad que la varianzas poblacionales sean diferentes; esta información es importante ya que si se estiman iguales se usa un procedimiento estadístico para calculat t y si las varianzas son distintas se utiliza una variante en la fórmula. Al observar la tabla notamos que el valor para "Sig." es 0,551 que es superior a 0,05. Esto significa que existe un 55% de probabilidades de que ambas varianzas sean iguales; porcentaje muy superior al 5% acordado en las ciencias sociales. Por lo tanto, para continuar la lectura de la tabla debe observarse los valores de la primera línea correspondientes a "Equal variances assumed" (Varianzas iguales asumidas). El siguiente valor es el de t = - 2,706. Este valor puede considerarse análogo al valor Z de una distribución normal. Usando una tabla de t student es posible ver si este valor se encuentra en el rango de 5% de probabilidad de ocurrencia en la distribución t correspondiente (ver tabla o usar calculadora). La distribución t es un poco distinta a la distribución normal, ya que es una distribución estimada a partir de datos muestrales. Esta estimación es penalizada en función del tamaño de la muestra. Así mientras más pequeña es la muestra mayor es la pena. Por esto - a diferencia de la distribución normal que se construye a partir de dos parametros: media y desviación estándar - la distribución t requiere conocer los "grados de libertad" (degrees of freedom). En nuestro caso esto se calcula restando al numero total de sujetos el numero de grupos, en nuestro caso son 80 sujetos en dos grupos: 80-2 = 78.
Conociendo los grados de libertad y la probabilidad 0,05% es posible ver la Tabla de la t de student y encontrar el valor t crítico. Buscamos en la tabla el valor de p = 0.05 para 78 grados de libertad. Esta tabla no muestra valores para 78 grados de libertad, se salta de 60 a 120. En este caso asumamos el valor correspondiente a 60 grados de libertad, una medida que hace más estricto el análisis; el valor t de la tabla es 2.0. Como el 0.05 se distribuye a ambos lados de la distribución; un valor tendrá menos de un 5% de probabilidades de ocurrir si cae bajo -2,0 o encima de 2. Puesto que nuestro valor (- 2,706) es menor que el valor t de la tabla (aún siendo más rigurosos de lo necesario) podemos concluir que las medias de los grupos son significativamente diferentes. Para conocer el valor exacto del t crítico puede usarse también el siguiente applet que dará como resultado un valor de -/+ 1.991, lo que permite sacar las mismas conclusiones ya señaladas.
Esta búsqueda del valor t de tablas o su cálculo en el applet se han planteado para comprender mejor el razonamiento estadístico, sin embargo, SPSS nos permite identificar si las diferencias son o no significativas directamente pues nos entrega el valor de la probabilidad -"Sig. (2-tailed)" - para el valor t obtenido. Así el valor el valor de p o la significación estadística es de 0,008 valor mucho menor a 0,05, lo que significa que existen muy pocas probabilidades que las muestras vengan de una misma población.
El procedimiento correcto para usar una t de student requiere que se planteen primero las hipótesis y estas son las que se sometren a prueba. En nuestro caso las hipótesis serían:
Hipótesis nula: No existen difrencias significativas entre la estatura promedio los grupos (o diciéndolo de otra manera: ambos grupos pertenecen a la misma población). p >= 0,05
Hipótesis experimental: Existen diferencias significativas entre la estatura promedio de los grupos (o diciéndolo de otra manera ambos grupos pertenecen a la distintas poblaciones). p<0,05
Los resultados de nuestro estudio nos llevarían a rechazar la Hipótesis nula y aceptar la Hipótesis experimental.
Álvaro Carrasco
UAH-2003